If you’ve ever tried to reconstruct – or even predict – the behavior of a time series, you understand how hard of a task it is. Ask any engineer or scientist: transient modeling, also known as time-domain modeling, is one of the biggest challenges in the modeling world. But it also presents a very interesting and exciting opportunity.
What is Transient Modeling?
First, let’s level-set on a definition: Transient modeling refers to the process of simulating and analyzing phenomena that vary over time, otherwise known as dynamic systems. Put like this, it’s a pretty simple concept. More advanced definitions would involve differential equations and fundamentals of dynamics, but we’ll save that for another time.
ou could argue that almost every physical process is transient, and you would be right. The overwhelming majority of physical processes that we can observe are transient systems. Weather patterns? Transient. Biological systems? Transient. Electric power grids? Transient. Traffic flow? You guessed it, transient.
With applications in design optimization, model calibration, and real-time control, transient modeling has become a major focus for the machine learning community. It enables engineers and scientists to make informed decisions and design better solutions for complex, real-world, industrial problems. Additionally, driven by advances in computational power, modeling techniques, and the increase in data availability, transient modeling has enabled new capabilities such as uncertainty propagation, sensitivity analysis, robust control, and more.
The list of industrial applications is nearly limitless. With such a huge variety of applications, where should you start? What modeling strategy should you use? Which tools should you pick? Even if you are only interested in steady-state or static values, those originate from transient behaviors.

Transient Modeling Methodologies
There are two popular transient modeling methodologies — a simpler solution that relies on data-focused tools and a more sophisticated solution based on physics principles. As engineers, we typically value simpler solutions wherever possible, but it is of paramount importance to understand the advantages and limitations of each approach.
The Data Scientist’s Methodology: Time Series Analysis
If you are familiar with the terms “seasonality,” “trend,” or “data correlation,” you may also be familiar with modeling transient time series using classical data science methods. The time series analysis approach focuses on statistical techniques and regression methods to analyze and model transient behavior. It involves the exploration of historical data to identify patterns, trends, and correlations within the time-dependent variables. Time series models aim to capture the statistical properties of the data, enabling the prediction of future values based on past observations. This approach is particularly useful when dealing with noisy real-world data, like brain or heart rate monitoring, and cyclical patterns, like temperature readings, where the underlying physical processes may not be fully understood or easily modeled.
While straightforward, this approach has limited real-world applications. It usually fails to capture the intrinsic physical processes that underpin dynamic systems. Time series are, first and foremost, simple observations from a human perspective. In reality, a deeper, more complex dynamical behavior needs to be unraveled to fully apprehend the system at hand in order to unlock progress on design & operational use cases that the industrial world needs.
To illustrate this, consider the motion of celestial bodies, such as planets, moons, and artificial satellites, all governed by the laws of orbital mechanics. While the observed behavior of objects in space may seem simple (such as regular orbits or gravitational interactions), the underlying dynamics involve complex gravitational forces and perturbations from other celestial bodies. The need for more sophisticated dynamical models is critical to predict and control spacecraft trajectories.
The Engineer’s Methodology: Dynamical System Modeling
State-space based dynamical modeling is an approach that seeks to understand physical processes and involves a more subtle perspective. It develops mathematical representations that describe the fundamental physics of the underlying system, such as position, velocity, temperature, and pressure fields.
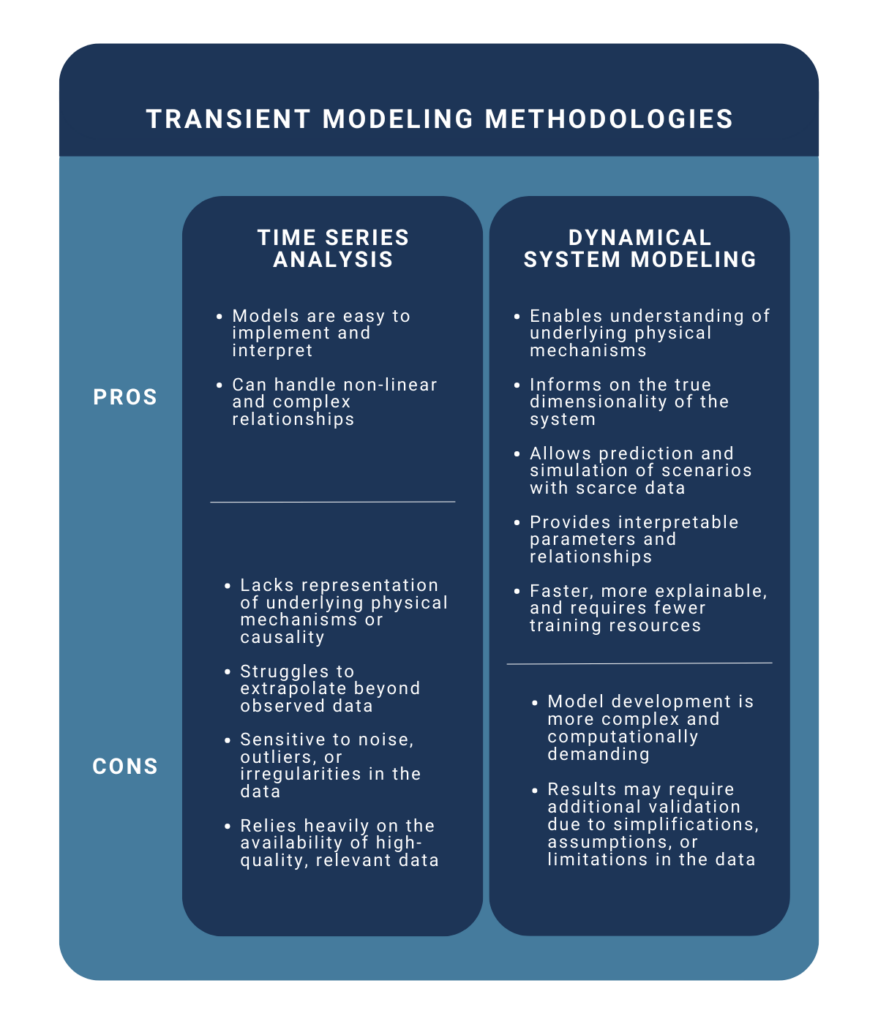
This approach relies on and domain-specific knowledge to construct mathematical models that simulate transient behavior. These models typically involve differential equations or other mathematical formulations that capture the relationships and time evolution between variables and the governing principles of the system. By explicitly representing the physical processes, this approach provides deeper insights into the mechanisms driving the transients and allows for more accurate predictions, analysis, and control of the system.
Transient Modeling in Action: Lorenz Oscillator Example
As an illustration, let’s compare the two methodologies using the classic problem of the Lorenz Oscillator. The Lorenz oscillator is a mathematical model that describes a simplified system of three coupled nonlinear ordinary differential equations. It was introduced by Edward Lorenz in 1963 to study atmospheric convection, but it has found applications well beyond meteorology.
The Lorenz oscillator has been widely used in the field of chaos theory and nonlinear dynamics. It is a classic example of a chaotic system, exhibiting sensitive dependence on initial conditions. The oscillator’s behavior, known as the “butterfly effect,” demonstrates how small changes in the initial conditions can lead to drastically different outcomes over time. This property has been instrumental in studying complex phenomena, such as weather patterns, fluid dynamics, and population dynamics. Its chaotic nature has been leveraged to improve the security of data encryption algorithms and enhance random number generation techniques. Additionally, the oscillator’s ability to capture intricate patterns of behavior has found applications in signal processing and image recognition.
The objective here is to predict the trajectory of the oscillator given two seconds of training data. Using the time series analysis modeling technique, trends, and repeatable patterns are identified and propagated at future times. This first approach (top chart) will only be able to learn from past observations and therefore predict future values using solely recent history. This is why we observe a wrong prediction past two seconds. On the other hand, the dynamical system modeling approach (bottom chart) allows the analyst to capture the actual dynamics of the Lorenz oscillator. The true dynamics of the Lorenz oscillator are identified and future time prediction recovers the famous two-lobe structure of the nonlinear oscillator.
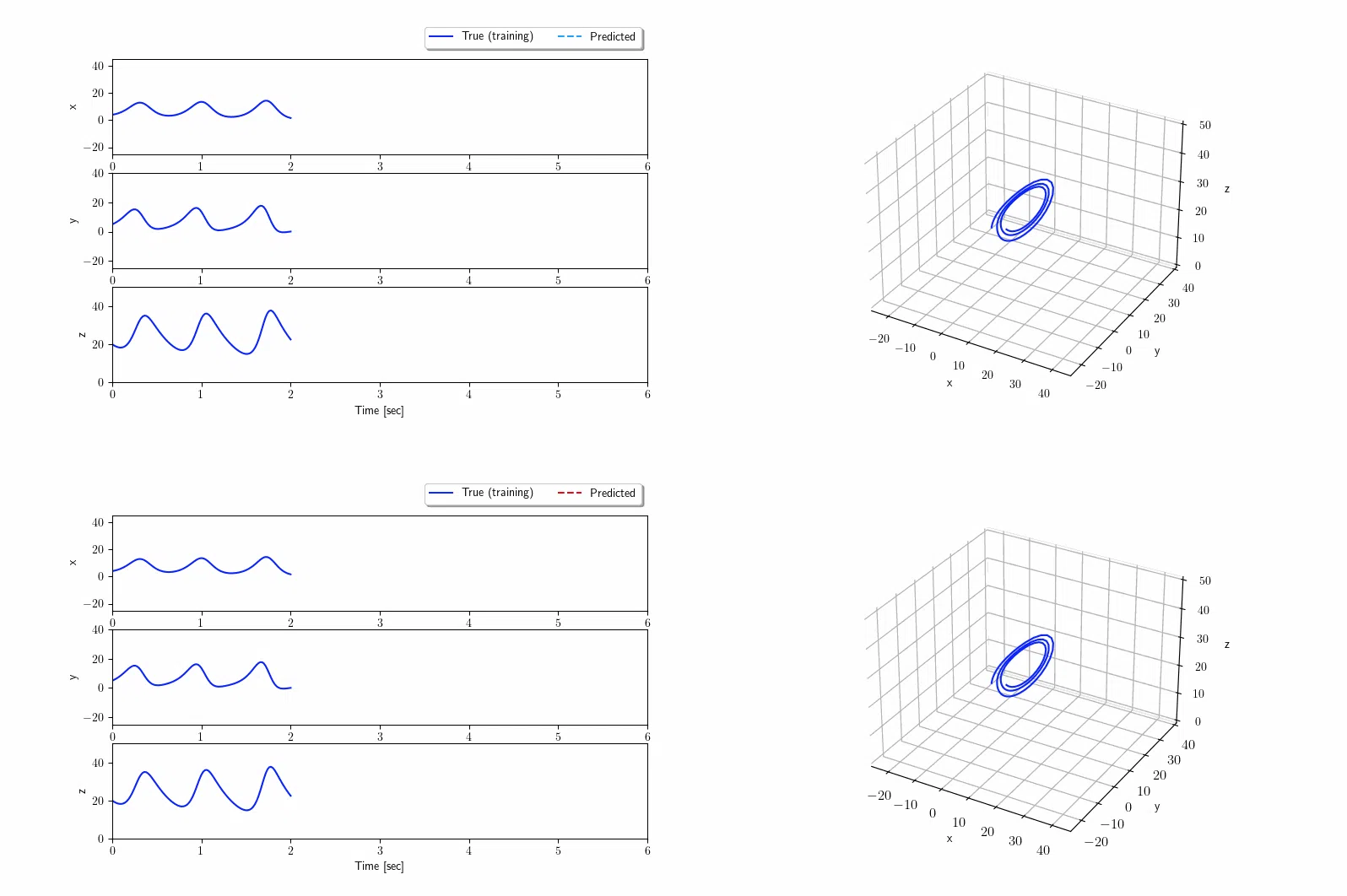
Linking this example to industrial problems, it is crucial to be able to identify the dominant features (dynamics) of a system rather than only the apparent structure of the data.
Achieving Industry-Ready Transient Modeling
At Geminus, we are working to advance transient modeling techniques and deliver tools to pursue the ambition of complete unsupervised modeling of dynamical systems. We are enhancing transient modeling techniques with machine learning (ML) to enable scalable methods that:
- Significantly reduce the computational expense of simulation-quality insights
- Can handle a huge variety of dynamical systems
- Are agnostic to the underlying physical process
- Learn the underlying dynamics of real systems
Our unified methodology consists of a combination of tools to derive accurate mathematical models for predicting the transient behavior of a wide range of industrial systems, with models that are computationally inexpensive and amenable to optimization and control.
The next frontier of modeling industrial processes is capturing the true transient behavior of real systems, unlocking advancements in process optimization, emissions reduction, and predictive maintenance. Understanding the tools at our disposal – and where they work best – is critical to making this vision a reality.


